Bonus - Solution to A Physics Problem

 

       Hello everyone, welcome back to my blog. This is just a bonus post, so I'll be solving only one question today in physics. That being said, let's get back to it.

Question

1.  Two mass 6kg and 4kg hung on a frictionless pulley with an inextensible string: 

a)  find the acceleration

b)  tension of the string

                                         (g=10m/s²)

   Solution

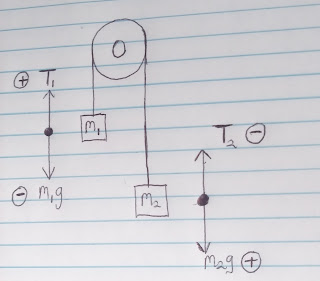
        To solve this question, you should at least have a basic knowledge or an idea on the Forces and Pulley system. That would help you understand this solution. From the question, we were given two masses 6kg and 4kg respectively. Suppose the small m represents the 4kg mass and the M represents the 6kg mass, the whole system would move to the right as seen in the picture below.

Force Diagram 

        The system doesn't have x-components (horizontal forces) because it's only moving in the y-direction (vertical forces). So, all we need to sum up the forces in the y-component for each masses. The net or resultant equation would help us get the acceleration of the system. 

Note: We would be using Newton's Second Law of motion which can be resolved to the simple formula F = ma; where m is the mass and a is the acceleration.

 

Let Tension on the 4kg mass be T1 and the force of gravity be m1g.

Let Tension on the 6kg mass be T2 and the force of gravity be m2g.

Let the acceleration on the two masses be a1 and a2 respectively.

      Also, any force that is in the direction of the system will be positive and any force that opposes the  direction of the system will be negative as shown below:

      Now, these are the net forces acting on block 1 and 2 respectively;

T1 - m1g = m1a1 - - - - - - - - - - - - - - - - - - (i)

m2g - T2 = m2a2 - - - - - - - - - - - - - - - - - -  (ii)

    Add equation (i) and (ii) and solve for acceleration.

T1 + m2g - m1g - T2 = m1a1 + m2a2

       Since the two masses on the pulley system are attached to an inextensible string, the resultant tension would remain constant on every part of the string and the acceleration would be uniform. This means that:

T1 = T2 = T

a1 = a2 = ay

     So this implies that:

m2g - m1g = (m1 + m2) ay

.'. ay = g (m2 - m1) / (m1 + m2)

     Now that we have this, we can solve for acceleration asked in question (a).

        Now, question (b), to solve for tension, you can either use equation (i) or (ii). But it's easier to just use equation (i). Either way, you'll get the same answer. So, using equation (i);

 T = m1g + m1ay  - - - - - -(iii)

Substituting ay in equation 3, you'll have ;

 T = m1g + m1 (g(m2 - m1) / (m1 + m2))

  

        

        We can now solve for the tension of the string which is:

T = (4*10) + 4(10(6 - 4) / (4 + 6))

T = 48N

   .'. The tension of the string is 48N. Since the question specified that the string is inextensible, we don't need to worry about the elasticity of the string when solving this question. Also, the pulley system is frictionless, so we don't need to consider any frictional force opposing the motion of the system. Assuming the pulley is not frictionless and the string is elastic, then we'd need to consider these factors into the equation when solving this type of problem.

        

        And that's the end of problem-solving for this post. I hope you enjoyed it. Thanks for taking the time to read this post. Feel free to comment below about anything on this post. Subscribe and follow this blog for more posts like this in the nearest future.

                                                                       Sources

   

1.  Double Pulley System. (2020, September 29). Retrieved September 30, 2020, from http://www.ikonet.com/en/visualdictionary/science/physics-mechanics/double-pulley-system.php

2.  What is atwoods machine what is it used for? Give a brief explanation - Physics - TopperLearning.com: B1ln1rcc. (n.d.). Retrieved September 30, 2020, from https://www.topperlearning.com/answer/what-is-atwoods-machine-what-is-it-used-for-give-a-brief-explaination/b1ln1rcc

DISCLAIMER

All the contents on this blog including the text, layout, designs are owned by the google blogger app. All the images are from me except the two digital images from ikonet.com and Brainly website. All questions are from the *P.UTME CHAMPIONS GROUP* Facebook group. Contents may not be copied, reproduced, transmitted, distributed, downloaded, or transferred in any form or by any means without my permission. (For permission to reprint, please contact via Gmail at ibraheemrahman2001@gmail.com